近期题单一览 时间:20201102~20201120
✔hdu1061,求$n^n$的末尾数字
✔hdu3117,矩阵快速幂算Fib数列
✔hdu6030,递推数列转为矩阵,再进行快速幂取模
✔hdu1576,拓展欧几里得
✔hdu2588,欧拉函数复习
✔hdu5656,有关GCD的动态规划(另解:容斥)
✔poj2689,区间素数板子
✔hdu3792,素数打表可做
✔hdu2841,容斥原理
✔hdu4135,容斥原理
✔hdu1028,递归/DP/生成函数
✔hdu1521,指数型生成函数
✔hdu5673,卡特兰数+逆元
✔hdu2999,SG函数
✔hdu1527,威佐夫博弈
部分题解 HDU5656 这道题目有很多解法,可以动态规划,可以容斥原理,还可以莫比乌斯函数(这个我没写)。
思想比较妙,因为这些数字都很小,所以可以开一个桶把GCD值对应的方案数直接存到数组里,即num[gcd的值] = 方案数这样。而后,枚举gcd的值而不是去枚举方案,即可得出答案。
这种用桶去存储的思路在上次某道贪心题小结里面也有出现,上次是以其中一个变量为关键词排序,另外一个变量(数字很小)直接枚举,看桶里是否有可以取出来的元素。
定位好要用桶来解决问题之后就好办了。
如果选择动态规划,设置dp[前i项任意选择][选择出来的GCD值为j],有:
$i-1$中能够选出$j$来,则$i$也必定能够选出$j$来。
若当前枚举到的$j$能够在$i-1$下枚举出来,则$a[i]$参与后有贡献dp[i][gcd(a[i], j)]。
整理后,得到:
① $dp[i][j] = dp[i][j] + dp[i-1][j]$
② $dp[i][gcd(a[i], j)]=dp[i][gcd(a[i], j)] + dp[i-1][j]$
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 #include <bits/stdc++.h> #define maxn 1005 #define mod 100000007 using namespace std ;int gcd (int a, int b) return b ? gcd(b, a % b) : a; } long long t, n, a[maxn], dp[maxn][maxn];signed main (void ) scanf ("%lld" , &t); while (t--) { long long maxx = 0 ; memset (dp, 0 , sizeof (dp)); scanf ("%lld" , &n); for (register int i = 1 ; i <= n; i++) scanf ("%lld" , &a[i]), maxx = max (maxx, a[i]); for (register int i = 1 ; i <= n; i++) { dp[i][a[i]] = 1 ; for (register int j = 1 ; j <= maxx; j++) { dp[i][j] = (dp[i][j] + dp[i-1 ][j]) % mod; if (dp[i-1 ][j]) dp[i][gcd(a[i], j)] = (dp[i][gcd(a[i], j)] + dp[i-1 ][j]) % mod; } } int sum = 0 ; for (register int i = 1 ; i <= maxx; i++) sum = (sum + i * dp[n][i]) % mod; printf ("%lld\n" , sum); } return 0 ; }
当然,你也可以使用容斥原理。
定义$g[i]$为选择出来的数的GCD值为i的倍数的方案数。
由子集性质,可得方案数为$g[i]=2^{num[i]}-1$,$num[i]$为数组$a$中能够被$i$整除的数。
后面,枚举倍数$j$,求得$g[i] = g[i] - g[i*j]$,得到GCD值刚好为$i$的方案数。
后续统计答案即为$\sum i*g[i]$。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> #define maxn 1005 #define mod 100000007 using namespace std ;long long t, n, a[maxn], num[maxn], g[maxn];long long gcd (long long a, long long b) return b ? gcd(b, a % b) : a; } long long qpow (int a, int b, int p) if (b == 0 ) return 1 ; if (b == 1 ) return a; long long tmp = qpow(a, b / 2 , p); tmp = (tmp * tmp) % p; if (b & 1 ) tmp = (tmp * a) % p; return tmp; } signed main (void ) scanf ("%lld" , &t); while (t--) { memset (num, 0 , sizeof (num)); memset (g, 0 , sizeof (g)); scanf ("%lld" , &n); for (int i = 1 ; i <= n; i++) scanf ("%lld" , &a[i]); for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= 1000 ; j++) if (a[i] % j == 0 ) num[j]++; for (int i = 1 ; i <= 1000 ; i++) g[i] = qpow(2 , num[i], mod) - 1 ; for (int i = 1000 ; i >= 1 ; i--) for (int j = 2 ; j * i <= 1000 ; j++) g[i] = (((g[i] - g[i * j]) % mod) + mod) % mod; long long ans = 0 ; for (int i = 1 ; i <= 1000 ; i++) ans = (ans + i * g[i]) % mod; printf ("%lld\n" , ans); } return 0 ; }
这题的确是很不错的题目。
然后,据说能莫比乌斯反演…我还是先不写了,我现在太菜了呜呜呜。
POJ2689 区间素数模板。
筛选出$[1, \sqrt{max_{rt}}]$区间内的所有素数。如果是int范围内,大概就是五万内的素数。
利用这些素数对需要求的区间进行筛选标记。
不过我被一个小小的坑点坑到了,具体坑点看代码注释。
其他思路都很好理解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 #include <cstdio> #include <cstring> #include <algorithm> #include <cmath> #include <iostream> #define int long long #define maxn 5000005 using namespace std ;int lf, rt, cnt, isp[maxn], sp[maxn];bool iisp[maxn];
void euler (int lim) memset (iisp, true , sizeof (iisp)); iisp[1 ] = false ; for (int i = 2 ; i <= lim; i++) { if (iisp[i]) { cnt++; sp[cnt] = i; } for (int j = 1 ; j <= cnt && i * sp[j] <= lim ; j++) { iisp[i * sp[j]] = false ; if (i % sp[j] == 0 ) break ; } } } signed main (void ) euler(50000 ); while (~scanf ("%lld %lld" , &lf, &rt)) {
memset (isp, 0 , sizeof (isp)); if (lf == 1 ) isp[0 ] = 1 ; for (int i = 1 ; sp[i] * sp[i] <= rt && i <= cnt; i++) { int st = lf / sp[i];
while (st <= 1 || sp[i] * st < lf) st++; for ( ;sp[i] * st <= rt; st++) isp[sp[i] * st - lf] = 1 ; } int maxx = -1 , minn = (1 << 30 ), las = -1 ; int ma_l, ma_r, mi_l, mi_r; for (int i = 0 ; i <= rt - lf; i++) { if (!isp[i] && las == -1 ) las = i; else if (!isp[i] && las != -1 ) { if (i - las > maxx) { maxx = i - las; ma_l = lf + las; ma_r = lf + i; } if (i - las < minn) { minn = i - las; mi_l = lf + las; mi_r = lf + i; } las = i; } } if (!(~maxx)) printf ("There are no adjacent primes.\n" ); else printf ("%lld,%lld are closest, %lld,%lld are most distant.\n" , mi_l, mi_r, ma_l, ma_r); } return 0 ; }
HDU2841 这题有两种做法,一个是容斥原理,一个是莫比乌斯反演。
其中,在$n=m$时,可以转化为欧拉函数求解(典型题目参考”SDOI2008仪仗队“)。
其示意图如下:
该题存在$n \neq m$的情况,考虑容斥原理。
首先,只有坐标互质的点才能被看见。
简要证明如下:
假设坐标$(x, y)$不互质,可设$d = gcd(x, y)$,即存在$x’ = x / d$,$ y’ = y / d$,易得$(x’,y’)$会阻挡看向$(x, y)$的视线。
故得只有坐标互质的点才能被看见。
然后,问题转化为求互质坐标的数目。
互质相对来说比较难求,我们转化为求不互质的坐标。
先考虑简单一些的一维情况(HDU4135,该题弱化版):
$Problem:\ $求解$[1, m]$上所有能被$n$整除的点。
也就是求$\sum_{i=1}^{m} [gcd(n, i) = 1]$,其中$[表达式]$表示当括号内表达式为真时返回$1$否则为$0$。
不妨先对$n$分解质因数,得$p_1,p_2,p_3,…,p_n$。
然后,容斥开始,容斥的复杂度是$O(2^k)$,$k$为因子数,本题数据较小可以使用。
对于单一一个素数,贡献值为$\lfloor m/p_i \rfloor$,将其添加到答案中。
对于任意两个素数积,贡献值为$\lfloor m/(p_i * p_j) \rfloor$,将其从答案中减去(去重)。
对于任意三个素数积,贡献值为$\lfloor m/(p_i p_j p_k) \rfloor$,将其添加到答案中。
以此类推…
如果对这个过程不是很理解,可以手玩下面这道容斥的例题:
1 假设班里有10个学生喜欢数学,15个学生喜欢语文,21个学生喜欢编程,班里至少喜欢一门学科的有多少个学生呢?
设三个集合分别为$A,B,C$,则:
$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|$
通过这个例子可以很容易理解为什么上面容斥是这么做的。
推广后,可得当交起来的集合数量是偶数时为减去贡献值,交起来的集合数量是奇数时为加上贡献值。
明白原理后,就可以开始写代码了。
既然是一个类似取或不取(质因数)的问题,那么就可以利用二进制来表示,1代表取该因子,0代表不取,枚举每一个状态,其中利用$lowbit$和对数确定取得是哪个集合,将它的贡献值乘上去(即求$p_ip_j p_k*…p_?$这样子)。
具体实现看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> #define maxn 100005 #define int long long using namespace std ;int lowbit (int x) return x & (-x); } int cnt_one (int x) int cnt = 0 ; while (x) x -= lowbit(x), cnt++; return cnt; } int bas[maxn];int calc (int n, int m) bas[0 ] = 0 ; int f = 0 ; for (int i = 2 ; i * i <= m; i++) { if (m % i) continue ; while (m % i == 0 ) m /= i; bas[++bas[0 ]] = i; } if (m > 1 ) bas[++bas[0 ]] = m; for (int i = 1 ; i <= (1 << bas[0 ]) - 1 ; i++) { int flag = cnt_one(i) & 1 ? 1 : -1 ; int now = 1 , tmp = i; while (tmp) { now *= bas[(int )log2(lowbit(tmp)) + 1 ]; tmp -= lowbit(tmp); } f += flag * (n / now); } return n - f; } signed main (void ) int t, cases = 0 ; scanf ("%lld" , &t); while (t--) { int a, b, m; scanf ("%lld %lld %lld" , &a, &b, &m); printf ("Case #%lld: %lld\n" , ++cases, calc(b, m) - calc(a-1 , m)); } return 0 ; }
至于难一点的二维情况,由于数据较小,可以直接枚举每一个一维情况,就能得到答案。
这里不再叙述。
除了使用普通的容斥原理,还可以使用莫比乌斯反演(这也是容斥推导出来的)。
该题实际上就是求:$\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i, j) = 1]$
实际上,这条式子(求互质数数目)是非常常用的。
关于反演的前置知识此处不做叙述,直接开始推式子(假设$n \leq m$):
$\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i, j) = 1]$
$=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{d|gcd(i, j)}μ(d)$
$=\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{d=1}^{n}μ(d)*[d|gcd(i, j)]$
$=\sum_{d=1}^{n}μ(d)\sum_{i=1}^{n}\sum_{j=1}^{m}[d|gcd(i, j)]$
$= \sum_{d=1}^{n} μ(d) \frac{n}{d} \frac{m}{d}$
推到这里就可以数论分块了。
做一个莫比乌斯函数的前缀和,就可以在$O(\sqrt n)$的复杂度中完成该题了。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 #include <bits/stdc++.h> #define maxn 100005 #define int long long using namespace std ;int t, n, m;int cnt, mu[maxn], pri[maxn], sum[maxn];bool isp[maxn];void euler (int lim) memset (isp, true , sizeof (isp)); isp[1 ] = false ; mu[1 ] = 1 ; sum[1 ] = 1 ; for (int i = 2 ; i <= lim; i++) { if (isp[i]) { pri[++cnt] = i; mu[i] = -1 ; } for (int j = 1 ; j <= cnt && pri[j] * i <= lim; j++) { isp[pri[j] * i] = false ; if (i % pri[j] == 0 ) break ; mu[pri[j] * i] = -mu[i]; } sum[i] = sum[i-1 ] + mu[i]; } } signed main (void ) euler(100000 ); scanf ("%lld" , &t); while (t--) { scanf ("%lld %lld" , &n, &m); if (n > m) swap(n, m); int ans = 0 , r; for (int i = 1 ; i <= n; i = r + 1 ) { r = min (n / (n / i), m / (m / i)); ans += (sum[r]-sum[i-1 ])*(n/i)*(m/i); } printf ("%lld\n" , ans); } return 0 ; }
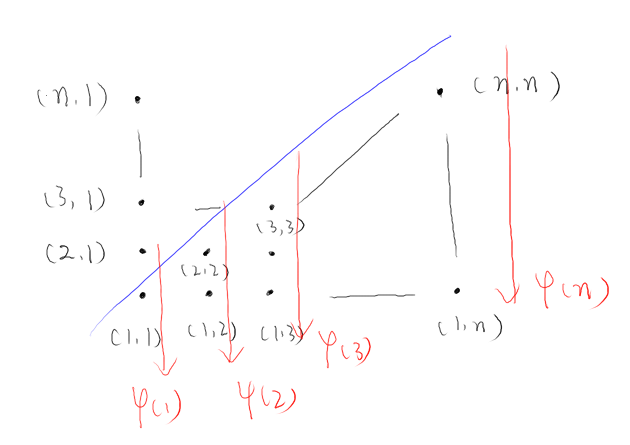
HDU1028 递推/记忆化搜索/生成函数均可做。
首先写一下记忆化搜索的思路,设立状态$dp[n][m]$。
具体意义,利用另一个相同的例题(POJ1664)理解更容易。
即设$n$为苹果数目,$m$为碟子数目,$dp[n][m]$为将$n$个苹果分到$m$个碟子中的数目,允许有空碟子。
开始分类讨论:
【边界情况】当$n=0$时,即没有苹果了,方案数为$1$。
【边界情况】当$m = 1$时,即只有一个碟子,方案数也为$1$(全都放到一个盘子里)。
当$n < m$时,即不可能放完所有的盘子,此时方案数与$(n, n)$相同(不计顺序)。
当$n \ge m$时,此时分为两种情况,存在空盘子和不存在空盘子:
存在空盘子时,方案数与$(n, m-1)$相同,即$m-1$个盘子均放满,或存在空盘子。
不存在空盘子时,方案数与$(n-m, m)$相同,即每个盘子都至少放了一个苹果。
由此写出对应的转移方程即可。
记忆化搜索代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 #include <bits/stdc++.h> #define maxn 1005 #define int long long using namespace std ;int n, dp[maxn][maxn];int solve (int n, int m) if (n == 0 || m == 1 ) return dp[n][m] = 1 ; if (dp[n][m]) return dp[n][m]; if (n < m) return dp[n][m] = solve(n, n); if (n >= m) return dp[n][m] = solve(n-m, m) + solve(n, m-1 ); } signed main (void ) while (~scanf ("%lld" , &n)) printf ("%lld\n" , solve(n, n)); return 0 ; }
一个道理,可以改写成递推形式:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 #include <bits/stdc++.h> #define maxn 1005 #define int long long using namespace std ;int n, dp[maxn][maxn];signed main (void ) while (~scanf ("%lld" , &n)) { for (int i = 0 ; i <= n; i++) for (int j = 1 ; j <= n; j++) { if (i == 0 || j == 1 ) { dp[i][j] = 1 ; continue ; } if (i < j) dp[i][j] = dp[i][i]; if (i >= j) dp[i][j] = dp[i-j][j] + dp[i][j-1 ]; } printf ("%d\n" , dp[n][n]); } return 0 ; }
由这样的递推关系,我们还可以使用普通型生成函数来解决这个问题。
生成函数最重要的思想:把组合问题的加法与幂级数的乘幂对应起来。
罗勇军老师的书对这一块讲的很好,转载如下:
首先设计函数:
$g(x) = (x^{0 1}+x^{1 1}+x^{2 1}+…) (x^{0 2}+x^{1 2}+x^{2 2}) …$
即为:
$g(x)=(1+x+x^2+x^3+…) (1+x^2+x^4+…) (1+x^3+x^6+x^9+…) * …$
其中: 1}+x^{1 1}+x^{2 * 1}+…)$分别代表不用数字$1$,用一次数字$1$,用两次数字$1$,以此类推。
这样子,寻找$x^n$的系数,就是我们最后要找的答案。
这样的普通型生成函数用于解决组合问题,指数型生成函数用于解决排列问题。
在想不到动态规划的转移方程的时候,可以考虑用生成函数,思路更为直观清晰。
生成函数的解法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 #include <bits/stdc++.h> #define maxn 1005 #define int long long using namespace std ;int n, c1[maxn], c2[maxn];signed main (void ) while (~scanf ("%lld" , &n)) { for (int i = 0 ; i <= n; i++) c1[i] = 1 , c2[i] = 0 ; for (int k = 2 ; k <= n; k++) { for (int i = 0 ; i <= n; i++) for (int j = 0 ; j + i <= n; j += k) c2[i + j] += c1[i]; for (int i = 0 ; i <= n; i++) c1[i] = c2[i], c2[i] = 0 ; } printf ("%lld\n" , c1[n]); } return 0 ; }
HDU1521 指数型生成函数板子题。
假设有两个物品$A$,构造如下:$(\frac{1}{0!}+\frac{x}{1!}+\frac{x^2}{2!})$,其中各项系数(此处均为$1$)代表选$k$件A的排列数,$k$为幂次。
另外,除以阶乘是因为要删除重复的排列,例如$A_1BA_2$和$A_2BA_1$是同一种方案,$A_1A_2$的排列数为$2!$,由此得到分母应为$2!$。
拓展到多个物品,两个物品$A$,三个物品$B$,一个物品$C$,构造生成函数如下:
$g(x)=(\frac{1}{0!}+\frac{x}{1!}+\frac{x^2}{2!}) (\frac{1}{0!}+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}) (\frac{1}{0!})$
最后,取幂次为$m$的项的系数,就是要求的答案。
阶乘需要特殊处理一下,处理乘法时直接除多一项,最后统计答案时再乘上$m!,$就可以化出对应答案。
具体看代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> #define maxn 100005 #define int long long using namespace std ;int n, m, a[maxn];double c1[maxn], c2[maxn]; double fl (int x) double tmp = 1 ; for (int i = 1 ; i <= x; i++) tmp *= i; return tmp; } signed main (void ) while (~scanf ("%lld %lld" , &n, &m)) { memset (c1, 0 , sizeof (c1)); memset (c2, 0 , sizeof (c2)); for (int i = 1 ; i <= n; i++) scanf ("%lld" , &a[i]); for (int i = 0 ; i <= a[1 ]; i++) c1[i] = 1.0 / fl(i), c2[i] = 0 ; for (int k = 2 ; k <= n; k++) { for (int i = 0 ; i <= m; i++) for (int j = 0 ; j <= a[k] && i + j <= m; j++) c2[i+j] += c1[i] / fl(j); for (int i = 0 ; i <= m; i++) c1[i] = c2[i], c2[i] = 0 ; } printf ("%.0lf\n" , c1[m] * fl(m)); } return 0 ; }
HDU5673 这题可以看成卡特兰数板子题的增强版,增加了可以原地不动的操作。
那么我们就可以,枚举到底左右各移动多少次(至多$\lfloor n/2 \rfloor$次),这部分是否合法用卡特兰数思路去做(同规范01序列那题 )。
就可以得到答案$\sum_{i=0}^{\lfloor n/2 \rfloor} C_{n}^{2i}*Catalan(i)$
这一题比较难的点,还是在逆元的求解。
逆元求解主流有四种考法,拓展欧几里得,费马小定理,线性求逆元,阶乘求逆元。
下面再简单总结一下:
拓展欧几里得
求解不定方程$ax+by=c$的特殊情况$(c = 1)$。
的逆元即为满足$ax \equiv 1(mod \ b)$的数$a$,这条式子又可转为$ax + by = 1$,因此可用$exgcd$求解。
费马小定理(求单个数的逆元,要求$a \perp p$,且$p$为素数)
使用这种情况求逆元时,只需求得$a^{p-2} \ mod \ p$。
由小定理,有$a^{p-1} \equiv 1 (mod \ p)$,
即有$a * a^{p-2} \equiv 1 (mod \ p)$。
故,$a^{p-2}$为$a$在$mod \ p$意义下的逆元,用快速幂求解即可。
线性递推(递推求一串数的逆元,例如$1-n$)
对于边界情况$x=1$时,$x^{-1} = 1$
对于其他情况$x=i$时,构造$p = i*k + r$
有$i*k+r \equiv 0(mod \ p)$
两边同乘$i^{-1},r^{-1}$,得$k*r^{-1}+i^{-1} \equiv 0 (mod \ p)$
移项,得$i^{-1} \equiv -k*r^{-1} (mod \ p)$
由题意,得$k = \lfloor {p/i} \rfloor, r = p \ mod \ i$。
代入,得$i^{-1} = - \lfloor p / i \rfloor * (p \ mod \ i) ^ {-1} $。
现实使用中,我们常常会使用$(p - \lfloor p/i \rfloor)$来避免负数!
由此式,即可线性递推逆元,也可以递归求解,将较大的数缩小到某个范围内 。
PS:据说这种递归求解方式上界约为$O(n^{\frac{1}{3}})$?
阶乘逆元
如果只是某个阶乘,可以用上面递归的方式去做,如果是求一串阶乘(以$0!-n!$为例)的逆元,则:
先用某种方法求出$n!$的逆元
由$\frac{1}{(n+1)!} (n+1)=\frac{1}{n!}$,得$inv[n] = inv[n+1] (n+1)$。
【因为逆元相当于求倒数,由此可以开始递推】
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 #include <bits/stdc++.h> #define maxn 1000010 #define mod 1000000007 #define int long long using namespace std ;int h[maxn], sum[maxn], ans[maxn], inv[maxn], cn[maxn], cm[maxn];int qpow (int a, int b) if (b == 1 ) return a; int tmp = qpow(a, b / 2 ); tmp = (tmp * tmp) % mod; if (b & 1 ) tmp = (tmp * a) % mod; return tmp; } int calc (int x) if (x < maxn-10 ) return inv[x]; return (calc(mod % x) * (mod - mod / x)) % mod; } int bin (int x, int y) return (((cn[y] * cm[x]) % mod) * cm[y-x]) % mod; } signed main (void ) ans[1 ] = 1 ; inv[1 ] = 1 ; h[0 ] = h[1 ] = 1 ; sum[0 ] = 1 ; sum[1 ] = 2 ; for (int i = 2 ; i <= 1000001 ; i++) inv[i] = ((mod - mod / i) * inv[mod % i]) % mod; cn[0 ] = cm[0 ] = 1 ; for (int i = 1 ; i <= 1000000 ; i++) { h[i] = ((((4 * i - 2 ) * inv[i + 1 ]) % mod) * h[i - 1 ]) % mod; cn[i] = (cn[i-1 ] * i) % mod; cm[i] = calc(cn[i]); } int t, n; scanf ("%lld" , &t); while (t--) { scanf ("%lld" , &n); if (ans[n]) { printf ("%lld\n" , ans[n]); continue ; } for (int j = 0 ; j <= n / 2 ; j++) ans[n] = (ans[n] + bin(2 *j, n) * h[j]) % mod; printf ("%lld\n" , ans[n]); } return 0 ; }
HDU2999 SG函数入门题。
需要注意,取的是连续的某一段石头,不一定是在两端取。
因此,存在这一回合取完石头后分裂为两个局势的情况,此时就要使用$SG$定理进行解决。
一般来说,推导$SG$函数有两种方法,一个是由小到大,直接递推,另一个是首先$SG$函数值初始化为$-1$,每次使用$dfs$求解(记忆化,若SG不为$-1$则直接返回)。
这里使用的是递推的方法,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 #include <bits/stdc++.h> #define maxn 100005 using namespace std ;int n, m, k, a[maxn], se[maxn];int s[maxn], sg[maxn];void SG () memset (sg, 0 , sizeof (sg)); for (int i = 1 ; i <= 1000 ; i++) { memset (s, 0 , sizeof (s)); for (int j = 1 ; se[j] <= i && j <= se[0 ]; j++) {
s[sg[i-se[j]]] = 1 ; int tot = i - se[j]; for (int k = 1 ; k <= tot - 1 ; k++) s[sg[k]^sg[tot-k]] = 1 ; } for (int j = 0 ; j <= 1000 ; j++) { if (!s[j]) { sg[i] = j; break ; } } } } int main (void ) while (~scanf ("%d" , &n)) { se[0 ] = 0 ; for (int i = 1 ; i <= n; i++) scanf ("%d" , &a[i]); sort(a+1 , a+n+1 ); for (int i = 1 ; i <= n; i++) if (a[i] != a[i-1 ]) se[++se[0 ]] = a[i]; SG(); scanf ("%d" , &m); for (int i = 1 ; i <= m; i++) { scanf ("%d" , &k); printf (sg[k] ? "1" : "2" ); putchar ('\n' ); } } return 0 ; }
HDU1527 威佐夫博弈入门题。
经典情形:
有两堆石头,两堆石头数目可以不同,每人轮流取石头
可以选择一堆石头拿走任意个石头
可以选择两堆石头拿走相同个石头
谁最后拿完谁赢
然后,若两堆石头差的绝对值乘上(1+sqrt(5))向下取整后,等于两堆石头中较小那堆石头的数目,则为奇异局势。奇异局势先手则必输,反之必胜。
关于证明暂时鸽鸽了,实在比较难弄。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 #include <bits/stdc++.h> using namespace std ;long long a, b;int main (void ) while (~scanf ("%lld %lld" , &a, &b)) { if (a > b) swap(a, b); long long c = b - a; long long ans = c * (1.0 + sqrt (5.0 )) / 2 ; printf ("%lld\n" , ans == a ? 0 : 1 ); } return 0 ; }