Codeforces 1528B - Kavi on Pairing Duty
条评论题意
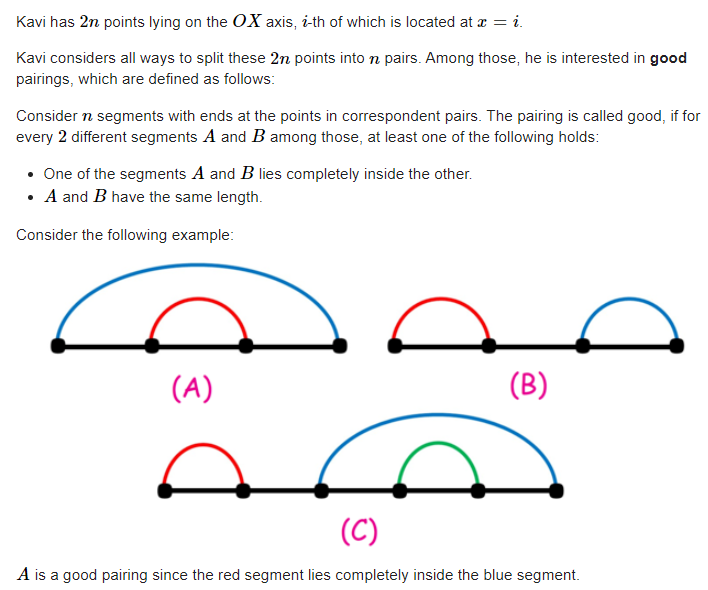
给定一个数$n$,代表数轴上有$2n$个点。你需要做$n$次操作,每次操作选择两个未被选择的点连在一起形成一条边。在执行完$n$次操作后,如果每两条边都满足长度相同(图B),或某条边完全在另外一条边下方(图A),那么这个方案就是可行的。
如图C,由于选择红色边和蓝色边时,上面两个条件都不满足,因此是一种不合法的方案。
现在要求出一共有多少可行的方案,由于答案可能很大,对$998244353$取模。
思路
首先,拿到这道题,发现很可能是道计数题,有某种递推关系然后便于取模,或者是一个快速幂套一个式子之类的玩意(
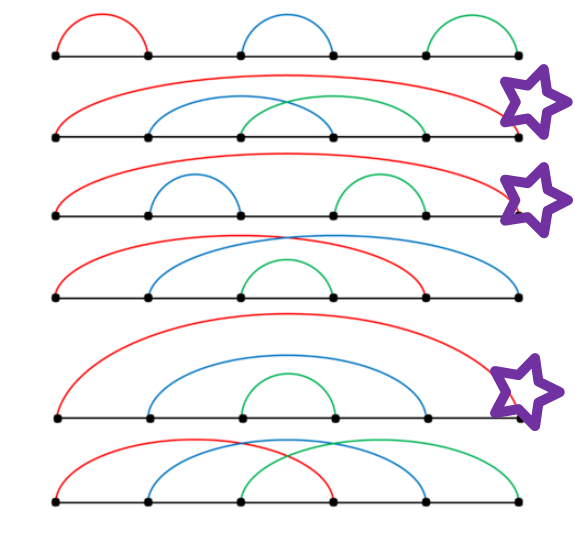
然后研究第二个样例($n=3$)的全部情况,发现有一种构造方法,即对于任意一个$n-1$情况下的合法解,在左右两边都插入一个点,并连线形成一条新的边,这样所得到的方案一定是合法的。见紫色星星标记的部分。
由此,开始考虑$dp$,看能不能从这里看出什么递推关系。
我们先考虑存在某个已经得到结果的方案,再考虑往两端插入新的点,从某一已知情况进行转移。
我们设置,对于某一个已经得到解决方案数目的情形$k_1$,两端插入各一个点。
此种情况下可以得到情况$k_1+1$中,由情况$k_1$转移过来的情况,有$1$种。
然后考虑,对于某一个已经得到解决方案数目的情形$k_2$,两端插入各两个点。
此种情况下可以得到情况$k_2+2$中,由情况$k_2$转移过来的情况,有$2$种。
但是我们发现,假设$k_2+2 = k_1 + 1 = G$,那么就存在一个重复的情况:
即在$k_2$转移到$G$的过程中,第一个点连接最后一个点,第二个点连接倒数第二个点,与$k_1$转移到$G$中的做法是等价的。
为了递推时不重复,我们可以规定,在两端各插入了$k$个点后,第$1$个点一定是连接第$2n + k + 1$个点,第$2$个点一定是连接第$2n + k + 2$个点,第$k$个点一定是连接第$2n + k + k$个点。
由此,我们得到这种情况下的递推方程:
这一过程,我们可以使用前缀和优化,降低时间复杂度。
然后,我们考虑另外一种情形,那就是全部的连线长度相等。这种情况是不能进行转移的。
不能转移怎么办呢,我们需要对每一个$i$都单独计算这种情形下的可能性。
暂时没有发现怎么做,手推一下样例:
当$n=2$,$len=1,2$,可行。
当$n=3$,$len=1,3$,可行。
当$n=4$,$len=1,2,4$,可行。
其中,$len$为终点下标减去起点下标得到的长度。
由此观察,好像$\sum [len | n] \ $就是答案。
由此,使用欧拉筛递推求约数数量$d(n)$,即可得到这种情况下的答案。
交题的时候没有想明白为啥是$d(n)$,写了一发过了大样例,一交就过了(
正确性可以参考这一篇题解画的图:Codeforces Round #722 (Div. 2) D. Kavi on Pairing Duty(证明和公式图解)_jziwjxjd的博客-CSDN博客
他所使用的是$1 \rightarrow x$来表示连边,转化到我这里,$x-1$就代表$len$,也就是在那篇博客最后得到的结论中,$2n \equiv 0(mod \ 2x - 2) \Leftrightarrow 2n \equiv 0 (mod \ 2 * len)$。换言之,$len | n$成立。
综上所述,最终答案为:
结尾
快期末了(
感觉模电要挂((((