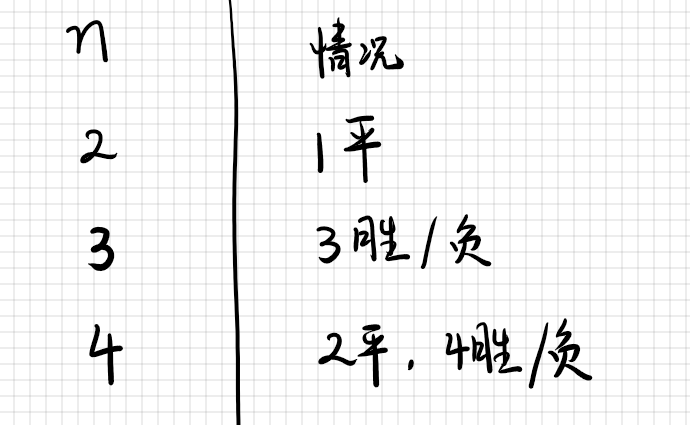
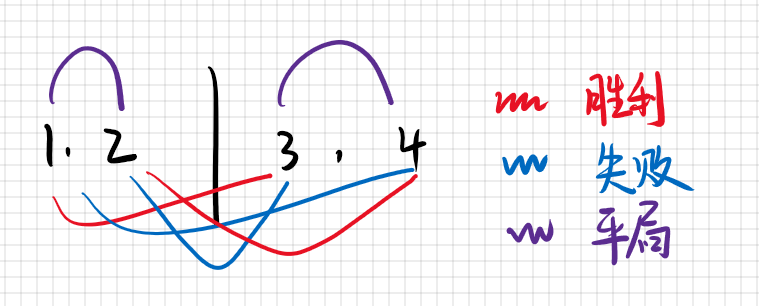
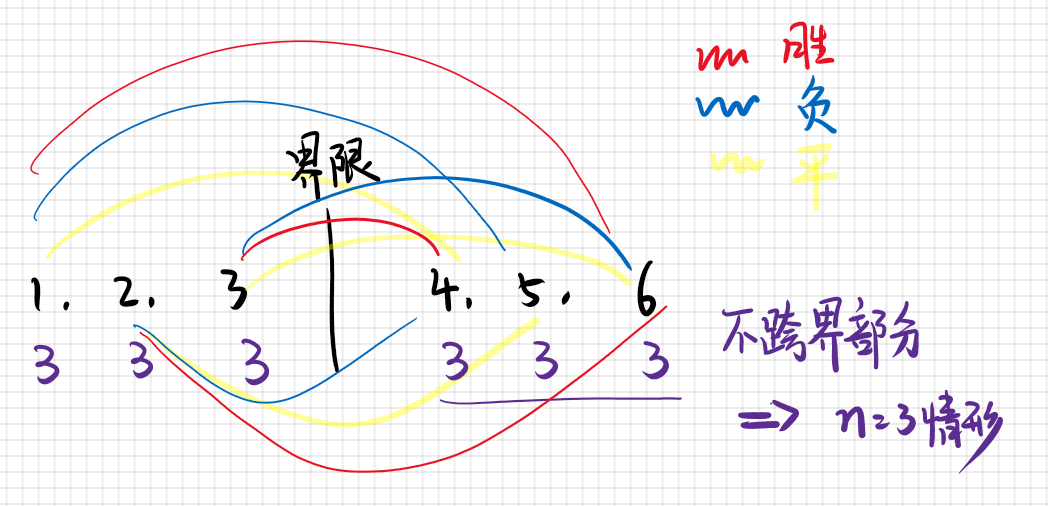
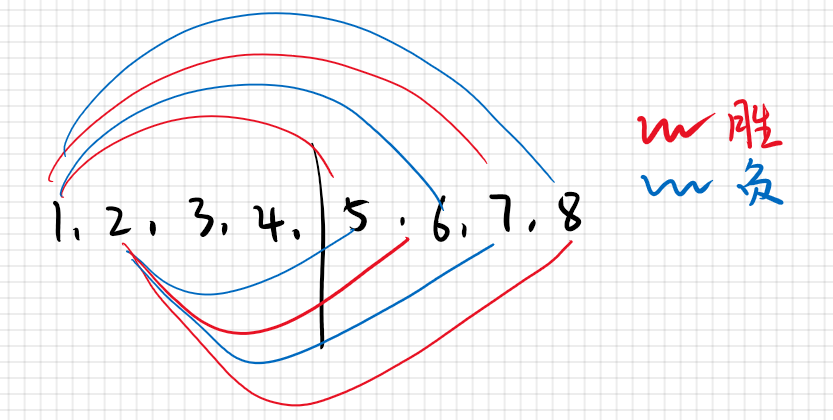题意

给定$n$支队伍，每支队伍都需要两两比赛一场。

如果某队伍得胜，则胜利队伍加三分，失败队伍不加分。如果平局，则两支队伍各加一分。

现在需要让你决定这$\frac{n(n-1)}{2}$场比赛的结果，使得平局最少的情况下，所有队伍得分相等。

image-20210603232116973

思路

首先，这大概率是一道构造题，需要找到一个方案构造答案使其满足题意。

于是，从较小的情况出发，如图：

image-20210603232900406

手模拟了$n$比较小情况下的最优解，考虑一下$n$更大的情况能不能由小情况构造而来。

image-20210603233335909

image-20210603234432951

我们发现，对于当前情形，我们可以分类讨论将他们分成若干小情形：

  • 当$n = 4$时，作为边界情况，直接如上图所示连边

  • 当$n$为偶数时，而且$n / 2$为奇数时，则需要最少$n/2$局平局。如$n=6$情况所示。

  • 当$n$为偶数时，而且$n/2$也为偶数时，我们可以对跨边界的情况直接进行胜负连边，然后递归求左右两部分的连边情况。

    image-20210603235125391

由于在这样分类情况下，我们每次连接时平局数目都是最小的，因此对于全局，这样构造出来的答案也是平局数目最小的解。

特别的是，我们还要考虑最开始$n$为奇数的情况。我们只需要胜负间隔着连接每场比赛即可，不需要平局。

由此即可编写代码$AC$。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
/* vegetable1024 | oi-liu.com | Maybe Lovely? */

#pragma GCC optimize("-fdelete-null-pointer-checks,inline-functions-called-once,-funsafe-loop-optimizations,-fexpensive-optimizations,-foptimize-sibling-calls,-ftree-switch-conversion,-finline-small-functions,inline-small-functions,-frerun-cse-after-loop,-fhoist-adjacent-loads,-findirect-inlining,-freorder-functions,no-stack-protector,-fpartial-inlining,-fsched-interblock,-fcse-follow-jumps,-fcse-skip-blocks,-falign-functions,-fstrict-overflow,-fstrict-aliasing,-fschedule-insns2,-ftree-tail-merge,inline-functions,-fschedule-insns,-freorder-blocks,-fwhole-program,-funroll-loops,-fthread-jumps,-fcrossjumping,-fcaller-saves,-fdevirtualize,-falign-labels,-falign-loops,-falign-jumps,unroll-loops,-fsched-spec,-ffast-math,Ofast,inline,-fgcse,-fgcse-lm,-fipa-sra,-ftree-pre,-ftree-vrp,-fpeephole2",3)
#pragma GCC target("avx", "sse2")
#define IO ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr)

#include <bits/stdc++.h>
#define maxn 205
using namespace std;
int t, n, ans[maxn][maxn];
void dfs(int lf, int rt){
    //printf("debug2: %d %d\n", lf, rt);
    int len = rt - lf + 1, nlen = len / 2;
    int mid = lf + nlen - 1;
    if(nlen & 1)
    {
        for(int i = lf; i <= rt; i++)
        {
            int flag = 1;
            for(int j = i + 1; j <= rt; j++)
            {
                if(j - i == nlen)    ans[i][j] = 0;
                else                 ans[i][j] = flag, flag *= (-1);
            }
        }
        return;
    }
    else if(nlen == 2)
    {
        int p1 = lf, p2 = lf + 1, p3 = rt - 1, p4 = rt;
        ans[p1][p2] = 0; ans[p3][p4] = 0;
        ans[p1][p3] = 1; ans[p1][p4] = -1;
        ans[p2][p3] = -1; ans[p2][p4] = 1; 
        return;
    }
    else
    {
        int flag = 1;
        for(int i = lf; i <= mid; i++)
        {
            for(int j = mid + 1; j <= rt; j++)
                ans[i][j] = flag, flag *= (-1);
            flag *= (-1);
        }
        dfs(lf, mid); 
        dfs(mid + 1, rt);
    }
}
int sc[maxn];
int main(void)
{
    scanf("%d", &t);
    while(t--)
    {
        memset(ans, 0, sizeof(ans));
        scanf("%d", &n);
        if(n & 1)
        {
            int flag = 1;
            for(int i = 1; i <= n; i++)
                for(int j = i + 1; j <= n; j++)
                    ans[i][j] = flag, flag *= (-1);
        }
        else    dfs(1, n);
        for(int i = 1; i <= n; i++)
            for(int j = i + 1; j <= n; j++)
            {
                if(ans[i][j] == 1)
                    sc[i] += 3;
                else if(ans[i][j] == -1)
                    sc[j] += 3;
                else
                    sc[i]++, sc[j]++;
                
                printf("%d ", ans[i][j]);
            }
        putchar('\n');
        /*
        printf("debug: ");
        for(int i = 1; i <= n; i++)
            printf("%d ", sc[i]);
        */
    } 
    return 0;
}

官方题解

题解的解法比我要精简的多，只需要讨论最开始时候$n$为奇数还是偶数就可以了=_=

这份题解对最小平局数的推导很不错。从假设没有平局出发，得到此时分数应为$\frac{3n(n-1)}{2}$。但由于分数应该整除$n$，因此需要求解最小的$t$，使得$\frac{3n(n-1)}{2} - t \ mod \ n = 0$。由此得到$t=\frac{n}{2}$。然后再从这个结论去进一步推导如何构造。

image-20210603235646917

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//@BledDest
#include<bits/stdc++.h>

using namespace std;

int main()
{
    int t;
    cin >> t;
    for(int i = 0; i < t; i++)
    {
        int n;
        cin >> n;
        if(n % 2 == 1)
        {
            for(int i = 0; i < n; i++)
                for(int j = i + 1; j < n; j++)
                    if(j - i <= n / 2)
                        cout << 1 << " ";
                    else
                        cout << -1 << " ";
            cout << endl;
        }
        else
        {
            for(int i = 0; i < n; i++)
                for(int j = i + 1; j < n; j++)
                    if(j - i < n / 2)
                        cout << 1 << " ";
                    else if(j - i == n / 2)
                        cout << 0 << " ";
                    else
                        cout << -1 << " ";
            cout << endl;
        }
    }
}

结尾

快期末了，长篇阅读还没写（

快$GDCDP$了，快蓝桥了，还啥都不会（

$GG$。